Аэродинамика экраноплана.
F
Fan-Fen2
Постановка задачи не конкретная - там только рисунок, который свидетельствует лишь о плохой подготовке форумчан с основами аэродинамического эксперимента и о некотором забытии основ аэродинамики (поток - струйка).
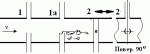
Вот более понятный вариант рисунка (не задачи!)
Опыи же ставить не буду - пусть Войцех попрактикуется.
Вложения
Начнем с конца. Сечение трубы постоянное? Да. Скорость распределена равномерно поперек? Да. Расход - их произведение. Из уравнения неразрывности он от начала трубы до ее конца измениться не может. Значит и скорость будет постоянной.
По Бернулли. А где я говорил, что давление на выходе (вне трубы) будет равно давлению на входе? Как раз наоборот. Я все время Вам толкую, что для того, чтобы появилось течение, надо на входе создать избыточное давление. Это Вы начали с того, что давление во всей трубе будет атмосферным.
По Ньютону. Мы выяснили (надеюсь), что скорость на входе и выходе будет одинаковой. Значит ускорение равно нулю.
Я правильно понял, что Вы предлагаете заменить одно торцевое отверстие двумя на боковых поверхностях? А какая разница? Там на цилиндре как раз максимальное разряжение. ;D
Но поскольку эжекции нет, ничего не изменится. Т.е. разницы - никакой.
Единственный профит, который приходит в голову, что в случае неточной (на 2-3 градуса) ориентации трубки в потоке погрешности в Вашем случае взаимно компенсируются.
lav
Я люблю строить самолеты!
Вы что специально дурика валяете!!! 😡 Чего свалили в одну кучу?!!! Мы сейчас рассматриваем два варианта течения в трубе : 1-течение по инерции условившись что жидкость идеальная тогда давление на входе не нужно и скорости на входе и выходе будут одинаковыми....и 2-течение когда к входу приложено избыточное давление...так вот в этом случае скорость на выходе не может быть равна скорости на входе....потому что полные
давления на входе и выходе не могут быть разными! Во втором случае жидкость тоже идеальная.
Вы не сделали того, что я просил: п.1
Когда Вы разберетесь с этими формулами, то поймете, что все, что написано в п.2 - правильно. И никаких ускорений там нет. Или покажите мне в формуле, чему равна величина ускорения.
Можете привести свои формулы, описывающие это течение и опровергающие мою точку зрения. Обсудим.
И как Вы это представляете?
Мы (Вы), ведь, говорим(ите):
1. о горизонтальной трубе;
2. трубе равного сечения на входе и выходе;
3. четко не ясно, конец трубы -- это второе исследуемое сечение или выход в атмосферу?
lav
Я люблю строить самолеты!
Мне не надо ничего никуда подставлять...я априори знаю , что уравнение Бернулли справедливо только для установившегося течения при условии несжимаемости жидкости и неразрывности потока ...т.е. если сечение потока уменьшилось то жидкость не имеет права "прошмыгнуть" его сжавшись (удельный объём не должен измениться)...жидкость должна только ускориться а для ускорения нужна энергия (внутренняя энергия удельного объёма в этом сечении уменьшается) ...при прохождении расширившегося сечения жидкость не имеет права расшириться ...она должна только затормозиться с выделением энергии ...внутренняя энергия при этом восстанавливается...т.е. для первого случая ,для трубы постоянного сечения с давлением на выходе Р статическое давление по всей трубе тоже Р. Для второго случая ...если на входе трубы давление 2Р а на выходе Р ,и если предположить ,что скорость на входе равна скорости на выходе , то полное давление на входе ( 2Р+рV^2/2) не будет равно полному давлению на выходе (р+ рV2/2) т.е. это не наш случай ...это случай водяной пушки с ускорением заряда на длине трубы.
казак
Строю трансформер
- Откуда
- г.Волгоград
У меня нет своих законов , терминов и т.д. у меня есть представление как всё происходит и я не делю всех форумчан по "фонетическому "признаку, т.е на слух..А вот вы господа "учёные", похоже запутались в законах "глобализаторов" с их допущениями и условиями ..Например, споря о изменении Р ,скорости потока W и температуры Т и объёма V при обтекании профиля применяете закон сохранения энергии (закон замкнутой системы) ,
(http://ru.vlab.wikia.com/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D1%81%D0%BE%D1%85%D1%80%D0%B0%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F_%D1%8D%D0%BD%D0%B5%D1%80%D0%B3%D0%B8%D0%B8) И вот давайте смотреть дальше :прежде всего забудем про сжимаемость и трение , только в этих условиях можно следовать постулатам этого закона, а как же следовать , если изменение давления Р по сути предполагает наличие сжимаемости ? Закон оказывается (*по Бернулли) допускает небольшую сжимаемость, но оказывается уже без изменения объёма V ! Вот наставили сосен то ! Ну хорошо, сделаем в мозгах нужные галочки и поехали дальше..Вот бернуллиевский сосуд ,с тонким сечением посередине и с широкими по краям . Для осуществления движения нужно приложить давление на одном из концов, иначе ничего не произойдет ! Вот первое противоречие закона , который зиждется на замкнутости системы без поступления энергии из вне !Как же быть если в левой расширенной части сосуда давление больше - всё ! Закона нет! Закон утверждает, что в широких частях сосуда будет давление больше , чем в узком, и по закону сохранения в одинаковых широких давление должно остаться одинаковым ! Но в жизни так не будет! Почему ? По качену , потому что закон не учитывает силы трения возникающие в процессе , отсюда закон не учитывает изменения температуры, сопутствующей силам трения, а та в свою очередь тянет на себя изменение объёма и пошло и поехало !И все эти величины, как заметил Лав, изменяются со скоростью звука, со своими линейными и временными градиентами! Вот уже и не 3 сосны расставлено , в которых немудрено запутаться "учёным " мужъям, куда уж "казакам" то разобраться 😉 И вот каким нужно быть изощрённым "учёным" ,чтобы выиграть в этом споре? Только авторитетом,которому поверят на слово, и так это всё 300-400 лет держится ИМХО..Куда уж нам казакам ! Я постою в сторонке и посмотрю, кто же из вышеспорящих самый авторитетный ? :-?
F
Fan-Fen2
Как быть тогда с этой записью уравнения для сжимаемой жидкости? Она более общая и универсальная, хотя и не полная. На ней "держится" вся теория и практика ВРД...
Вложения
Как с такими тяжело. Вот, что он подразумевал? Потенциальную энергию? Или Казак ему так мозги вправил, что уже и "человека потеряли".
Она в газ превращается, или сечение, все-таки, -- не одинаковое?
lav
Я люблю строить самолеты!
Я уже ранее просил Вас не туманить мозги "казакам" поправками к закону....какие реальные расчёты ВРД!? Нам бы с трубами да крылом разобраться!
lav
Я люблю строить самолеты!
Теперь вся надежда только на Казака....может ему удастся и Вам вправить! ;D
казак
Строю трансформер
- Откуда
- г.Волгоград
@ ЖоржФеникс
А что , главный закон сохранения тоже подправили, или ещё не успели ? :-?
казак
Строю трансформер
- Откуда
- г.Волгоград
Градиент давления , вы какой имели ввиду? Вот одно определение :
Это как само изменение может отражаться ? @ PFELIX каламбурите? Я понял, что вы имели ввиду отражение давления с каким то линейным градиентом. убывания Р. Но тогда к вам возникает вопрос - при помощи какого физического лифта ( механизма) осуществляется это отражение Р ? Может быть вы имели ввиду это ? http://scask.ru/book_s_phis1.php?id=99
Ничего я не каламбурю. Вот мы и подошли к Рубикону. Перечитайте свои посты. Я хочу от Вас услышать:
1. давление;
2. импульс давления;
3. отражение ...;
4. механизм распространения давления;
5. ВП;
6. стационарная картина -- под крылом сформировалось поле давления и оно не меняется. Возможно градиент есть, но он тоже - НЕ меняется.
Вопрос, как Вы это все увязываете? Что отражается? Молекулы отскакивают от стенки, так это завсегда если, давление > 0.
казак
Строю трансформер
- Откуда
- г.Волгоград
Вы мне что, устраиваете экзамен ? Ещё пока не понятно кто кому должен его устраивать, вот мне понятны все процессы обозначенные у вас по пунктам. Я конечно не берусь блистать формулами и строить мат . модели. Что толку ,что некоторые из присутствующих это могут, а объяснить физ. суть воздушной подушки ВП, как она образуется и от чего зависит не могут..Итак начнём, поиграем немного в вопросики? Я первый задаю вопрос - так почему ВП теряется над травой, шероховатой поверхностью, или водой, по сравнению с ровной бетонной или асфальтовой поверхностью? Если это не так - обоснуйте или приведите пример..
F
Fan-Fen2
1. Где Вы видите поправки? Этот закон Думой не рассматривался, не утверждался... и ей не подвластен! ;D
2. Вы пытаетесь преподнести @казаку высшую математику не знакомя с арифметикой.
3. Теория ВРД - газовая динамика каналов...
ЗЫ: Есть две формы записи закона сохранения энергии - тепловая и механическая (Бернулли). В тепловой форме учитывается подводимая/отбираемая теплота в процессе (т.е. температурный фактор); в механической - подводимая/отбираемая механическая работа (напоры). Из первой записи имеем зависимость для температуры торможения, из второй - полного давления... по статическим параметрам и скорости потока.
Без знания этого, продолжайте трудную битву с прямой трубой. Весело наблюдать за эпистолярным творчеством.
lav
Я люблю строить самолеты!
Ну так помогите нам с прямой трубой !
