Правда и тут тоже придётся делать расчётец. Сами сделаете или доверите Владимиру(Карабас)?
Легко!
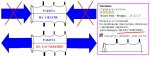
Рассмотрим сферу, внутри вакуум, снаружи давление «р» и плотность «ро нар», толщина стенки «s», плотность материала стенки «ро стенки», радиус «R»(много больше s). Площадь сферы: S=4*Пи*R^2 . Масса сферы: M=4*Пи*R^2 *s* (ро стенки) . Объем сферы: V=(4/3)*Пи*R^3. Подъемная сила: F=(4/3)*Пи*R^3*(ро нар).
Приравняем подъемную силу и массу получим: s*(ро стенки)=R*(ро нар)/3
Допустим, что «много больше»- это: R=10000* s (например радиус 10 м, толщина 1 мм), тогда ро стенки = (ро нар)*333,3
Плотность воздуха примем 1 кг/м3 , тогда плотность стенки 333,3 кг/м3 (0,33 г/см3, 0.000333 кг/см3)- что-то вроде пенопласта или бальсы!!!
Теперь рассмотрим сечение сферы диаметральной плоскостью. Площадь сечения (стенки) примерно будет равна: S=2*Пи*R*s , а сила давления (снизу и сверху) F=2*S*p= 4*Пи*R*s*p, заменив R=10000*s, получим: F= 4*Пи*10000*s^2*p, поделив на s^2, получим прочность стенки б=F/(s^2)= 4*Пи*10000*p, подставив давление 1 кг/см2, получим требуемую прочность стенки 120 000 кг/см2, а теперь найдем удельную прочность материала стенки: б/ро стенки= 120 000/0.000333= 3,6*10^8 (1/см), или 3,6*10^6 (1/м).
При таких величинах говорить о растяжении или сжатии, право- неловко!
Надо ли говорить, что материала, стакой удельной прочностью-не существует!!! :IMHO
Алё-ё-ё-ё , все ищем мою ошибку!!!
😉
Или плюем на вакуумный дирижабль, в статическом, надо заметить, виде. ;D