О подъёмной силе самолёта. Часть 1.

[Евгений055]

Лет 10 назад, занимаясь подготовкой конспекта лекций по практической аэродинамике для преподавания в аэроклубе, столкнулся с проблемой: Определение подъемной силы самолета, которое приводилось в доступных мне учебниках, не объясняет, что за подъемная сила держит самолет в воздухе, который выполняет перевернутый полёт со скольжением, например, и тем более что за подъемная сила держит самолёт в воздухе, который выполняет вираж с бочками….


Через несколько лет родилась небольшая научная статья, в которй приведены теоретические основы применения полярной и цилиндрической систем координат в аэродинамике и динамике полёта, с целью описания аэродинамических сил воз-действующих на высокоманевренный самолёт в полном диапазоне углов атаки и скольжения и во всех их взаимных сочетаниях.

Может быть, кому-то из читателей этого форума эта статья будет интересна.



1. Цилиндрическая скоростная система координат

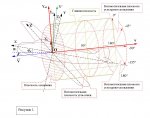
Главная ось цилиндрической скоростной системы координат Оv (далее главная ось) совпадает с вектором скорости невозмущенного потока.
Плоскость основания цилиндрической скоростной системы координат (далее плоскость основания) перпендикулярна главной оси и проходит через центр масс самолёта, где и лежит начало координат.
Плоскость вектора подъёмной силы самолёта, (далее плоскость подъём-ной силы) – плоскость перпендикулярная вектору скорости набегающего невоз-мущенного потока, совпадает с плоскостью основания цилиндрической скорост-ной системы координат.
Положение самолёта в воздушном потоке при использовании цилиндриче-ской системы координат полностью определяется углом атаки самолёта [ch945]с и уг-лом крена-скольжения [ch947]с. Здесь и далее маленькое С – « с  »   указывает на  ис-пользование цилиндрической системы координат.
За нулевое направление отсчёта крена-скольжения ОYc принимается на-правление проекции продольной оси Ox самолёта на плоскость основания. При угле атаки равном 0°, за нулевое направление для скоростной цилиндрической системы координат принимается направление оси ОY скоростной прямоугольной системы координат.
Плоскость, образованная нулевым направлением отсчёта и главной осью цилиндрической скоростной системы координат – главная плоскость.
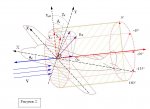
Угол крена-скольжения [ch947]с – отсчитывается от плоскости симметрии само-лёта (оси OY связанной системы координат) до плоскости, в которой лежит угол атаки самолёта (главная плоскость), в диапазоне от 0°до ±180°,  положителен при отсчёте против часовой стрелки, если смотреть по направлению полёта.
Угол атаки самолёта [ch945]с– угол между вектором скорости невозмущенного потока и продольной осью самолёта. Отсчитывается от 0°до 180°.

В случае, когда угол крена-скольжения равен 0° или 180°, главная плоскость совпадает с плоскостью симметрии самолёта и плоскостью XOY скоростной прямоугольной системы координат.
Вспомогательные плоскости угла крена-скольжения проводятся через главную ось и через вертикальную ось самолёта.
Вспомогательные плоскости угла атаки проводятся параллельно плоскости основания.
Главная плоскость и плоскость симметрии самолёта пересекаются по продольной оси самолёта.
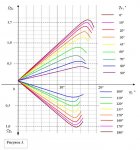
По главной оси откладывается значение угла атаки, при построении зависи-мости Сус и Схс от угла атаки, или значение коэффициента лобового сопротивления, при построении полной поляры самолёта.


Рис. 1. Цилиндрическая скоростная система координат.


Если связанная система координат неподвижна относительно самолёта, а скоростная система позволяет «отслеживать» вектор скорости полёта, привязывая при этом подъёмную силу к верхнему направлению вертикальной оси, то скоро-стная цилиндрическая система координат привязана к набегающему потоку и, в первую очередь, – к продольной оси самолёта.

 

[Евгений055]

2. Аэродинамические силы в цилиндрической
скоростной системе координат

В цилиндрической скоростной системе координат рассматриваются суммар-ная подъёмная сила самолёта Yc – проекция полной аэродинамической силы Ra на плоскость перпендикулярную вектору скорости набегающего невозмущенного потока и сила лобового сопротивления Xc – это проекция полной аэродинамической силы Ra на вектор невозмущённого воздушного потока.
Между плоскостью полной аэродинамической силы (YcORa) и главной плоскостью, будет возникать угол отклонения вектора суммарной подъёмной силы от главной плоскости [ch948]c – угол несимметричности обтекания.


Рис. 2. Схема сил, действующая на самолёт, в цилиндрической скоростной
системе координат, при установившемся движении


Суммарная подъёмная сила в цилиндрической скоростной системе координат будет соответствовать геометрической сумме векторов подъёмной и боковой сил скоростной прямоугольной системы координат:
__    __   __
Yс = Yа + Zа ;                                              (1.1)



или используя геометрический анализ:
            ________    
Yc =  [ch8730]Ya2 + Za2 ;                                         (1.2.)   

Сила лобового сопротивления в цилиндрической скоростной системе координат будет равна силе лобового сопротивления скоростной прямоугольной сис-темы координат.
                        __    __
                         Xс =  Xа  ;                                                   (1.3.)

Можно также записать следующее соотношение для основных углов:

[ch948]c = [ch947]с – arctg(Za / Ya) ;                               (1.4.)            

Выражая подъёмную и боковую силы прямоугольной системы координат через суммарную подъёмную силу Yc , можно получить:

Ya = Yc cos ([ch947]с – [ch948]c) ;                                 (1.5.)

Za = Yc sin ([ch947]с – [ch948]c) ;                                   (1.6.) 

Использование цилиндрической скоростной системы координат позволяет построить полные зависимости Сус и Схс от угла атаки самолёта при его обтекании воздушным потоком для различных углов крена-скольжения во всём диапа-зоне их возможных комбинаций, а также полную поляру самолёта для всех уг-лов атаки и углов крена-скольжения, получив при этом довольно наглядные графики в трёхмерном пространстве.

 

[Евгений055]

3. Зависимости коэффициента суммарной подъёмной силы
от угла атаки и угла крена-скольжения

Для построения полной зависимости Суc от угла атаки, необходимо при различных углах атаки поворачивать самолёт вокруг продольной оси на полный оборот, фиксируя при этом значение коэффициента суммарной подъёмной силы и отображая его на вспомогательных плоскостях, соответствующих углу крена-скольжения.
Семейство построенных графиков зависимости коэффициента подъёмной си-лы от угла атаки будет образовывать в скоростной цилиндрической системе координат поверхность зависимости Сус от угла атаки для различных углов крена-скольжения.
Если поворотом вокруг главной оси спроецировать пересечения вспомога-тельных плоскостей для заданных углов крена-скольжения и этой поверхности на главную плоскость, то можно получить примерно такое семейство графиков:


Рис. 3. Зависимость Суc от угла атаки для углов крена-скольжения в диапазоне от 0° до 180°


Пересечение главной плоскости и этой поверхности даст обычную зависи-мость Суc от угла атаки для прямоугольной скоростной системы координат.
На рис.3 приведена предположительная зависимость для углов крена-скольжения от 0° до 180°, с погрешностью 10-15%. За основу взята зависимость  Су от угла атаки для самолёта Як-52. [ch945]кр = 18,0°, Су макс = 1,56,  [ch945]0 составляет  –1°, для обратного полёта [ch945]кр = 15,0°, Су макс = –1,025.
На участке до появления местных срывов потока на крыле, зависимость будет линейной.
Диапазон углов атаки лежит в пределах от 0° до 180°. Понятие отрицательного угла атаки в цилиндрической скоростной системе координат теряет смысл.
Каждой комбинации значения угла атаки и угла крена-скольжения будет соответствовать своё значение угла отклонения вектора суммарной подъёмной силы от главной плоскости [ch948]c. Если значение [ch948]c лежит в диапазоне от 90° до 180° и от -90° до -180°, то создаётся отрицательная подъёмная сила.
Пересечение поверхности зависимости Сус от угла атаки для различных углов крена-скольжения и вспомогательных плоскостей угла атаки будет образо-вывать семейство кривых значений коэффициента суммарной подъёмной си-лы самолёта при неизменном угле атаки самолёта в зависимости от угла крена-скольжения в полярной системе координат. Примерный вид их приведён на рис.4.
По форме этих кривых можно предполагать о «мягкости» управления по крену – способности выдерживать горизонтальный полёт при изменении угла крена-скольжения (например, при выполнении «бочки»).


Рис.4. Кривые значений коэффициента суммарной подъёмной силы самолёта
при неизменном угле атаки самолёта в зависимости от угла крена-скольжения


Для маневренных самолётов построение этих зависимостей целесообразно не только для полётных углов атаки, но и для всего возможного диапазона. Построенная в цилиндрической скоростной системе координат, поверхность зависимо-сти Сус от угла атаки даёт наглядное представление о связи суммарной подъёмной силы с положением самолёта в воздушном потоке.
На кривой, соответствующей критическим углам атаки (обозначена красным цветом на Рис. 4.)  различными цветами продублированы участки, предположительно соответствующие появлению характерных зон при дальнейшем увеличении угла атаки:
- зона срыва потока, при попадании в которую самолёт начинает «парашюти-ровать» и поддаётся управлению (1);
- зона «сваливания самолёта на крыло» (2);
- зона срыва потока, при попадании в которую самолёт попадает в штопорное вращение (3);
- зона срыва потока, при попадании в которую самолёт попадает в «фюзеляжный штопор» (4);
- зона неупорядоченного вращения (5);
Точное расположение и размеры этих зон, по-видимому, можно будет определить только при продувке моделей самолётов в аэродинамической трубе.
Такие зоны будет более удобно рассматривать на поверхности зависимости Сус от угла атаки. На этой поверхности, также как и на поверхности полной поляры самолёта, можно выделить дополнительные характерные участки:
- граница возможной сбалансированности, которая определяет степень управляемости самолёта (для соответствующих скоростей полёта);
- граница критических углов атаки;
- зона ламинарного обтекания самолёта;


Рис. 5. Поверхность зависимости Сус от угла атаки


Используя аналогичные методы, можно построить зависимость Схс от угла атаки и угла крена-скольжения.


Рис. 6. Зависимость Схc от угла атаки для углов крена-скольжения в диапазоне от 0° до 180°


На мой взгляд, описание воздействия аэродинамических сил на самолёт в скоростной цилиндрической системе наиболее интересно для математического моделирования динамики полёта самолёта, применительно к авиационным тре-нажёрам и авиационным симуляторам. Возможно исследования, проведённые в этом направлении, позволят максимально приблизить поведение математической модели самолёта в воздухе к реальному поведению самолёта.

 

[Евгений055]

Рис.4. Кривые значений коэффициента суммарной подъёмной силы самолёта
при неизменном угле атаки самолёта в зависимости от угла крена-скольжения

 

[Евгений055]

Рис. 5. Поверхность зависимости Сус от угла атаки

 

[Евгений055]

Рис. 6. Зависимость Схc от угла атаки для углов крена-скольжения в диапазоне от 0° до 180°

 

[Миг-17ф]

А мне вот  на этой ветке никто вообще обснованно не ответил почем вообще подъемная сила возникает

http://www.reaa.ru/cgi-bin/yabb/YaBB.pl?num=1270401361/90

 

[mdp-shnik]

    Миг-17ф. Попробую ещё раз кратчайшим способом объяснить механизм возникновения подъёмной силы.

    На рис. 1 показан профиль крыла, обтекаемый идеальной жидкостью. Он не создаёт подъёмной силы.

    Когда есть вязкость и трение, погранслой на верхней поверхности профиля у его задней кромки не позволяет потоку перетечь с нижней поверхности  на верхнюю, как это показано на рис. 1. Виноват здесь пресловутый закон сохранения энергии, а конкретнее - закон Бернулли. При обтекании кромки скорость потока становится слишком большой, а давление в нём слишком малым. Погранслой со своим повышенным давлением и не пускает его туда.

   На рис. 2 показано обтекание профиля крыла реальным воздухом при большом угле атаки в момент начала движения. Справа имеем вихрь от срыва с задней кромки. Слева - ответный вихрь, который обязан обеспечить закон сохранения момента импульса. Если угол атаки достаточно мал, то этот вихрь не отрывается от профиля, а захватывает его собой. Снизу он уменьшает скорость потока, а сверху увеличивает. Вот вам и подъёмна сила.